一、陶瓷坯料配料的多目标规划模型

实际决策问题中有一类多目标决策问题，其评价决策效果的准则或决策系统希望达到的目标往往是多个。各目标间往往不可公度。因此，不存在通常意义下的最优解，也不能用一般解单目标问题的方法来解决，只能根据多个目标对决策人所产生的综合效用去评价决策方案的价值。问题的解只能是决策人认为“满意”的解，简称偏受解，而不是从无限或有限多方案中选出的最优解。本文所论的多目标规划法属于无限多可选方案中供决策人选择的一类。在进行多目标规划计算前，决策人应宣布其偏受意见。即给各目标排出一个优先等级次序。若同一级中有多个目标还应给出表示每一目标重要程度的加权系数。

此外还要给出各目标希望达到的目的值。在规划计算后，目标实际值可能达不到目的值，也可能会超过，因而目的值与实际值之间会出现正或负的偏差。于是，多目标规划变成了求出偏爱解，使目标的实际值与目的值间偏差为极小。目标按其重要程度排列了优先次序允许把多目标规划变成迭代计算单目标规划。陶瓷坯料配料问题可足够准确认为是个线性问题。于是，本问题变成为迭代求解线性规划问题。

陶瓷坯料配方是在若干种含有确定化学成分的原料中选择适当的比例而组成的。设原料库中可用原料的种数为n；原料中含化学成分的项数为p；陶瓷产品的种数为t；第j种原料中第k项化学成分的含量为akj；第j种原料在第I种产品的配方中的百分比含量为xij；第I种产品中第j项成分含量超过其目的值的正偏差变量为d+ji;第I种产品中第j项成分含量未达到目的值的负偏差变量为d-ji；第I种产品本次配料计划总用量为sI；第I种产品本次配料的期望成本为cI;第j种原料的成本cj；第j种原料的库存量为Qj。

一般认为，产品质量第一，保证质量前提下力求成本最低，最后是保证每次配料计算时库中有原料。现把目标分为三级。第1级目标p1有7个。即7个质量指标。1.SiO₂：2.Al₂O₃：3.灼减；4.KNaO；5.CaO；6.MgO；7.Fe₂O₃。第2级目标p2是成本。第3级目标p3取库存限量。同一级内各目标的加权系数为Wl,l=l，…，r。与正、负偏差变量对应分别写为W +l、W-l。各级目标函数必是相应偏差变量与加权系数的线性组合。整个规划的目标函数是各级目标函数之和。对具体问题，目标函数中的量可以简化。第m级目标的加权系数按如下规则选取：

当某质量指标取≤号，则Wlm>0，Wlm=0；

当某质量指标取≥号，则Wlm>0，Wlm=0；

当某质量指标取=号，则Wlm>0，Wlm>0；

设第1级的7个质量指标同样重要，则加权系数相同，令Wl1= Wl1=W1。第2级只一个目标，Wl2=W2。第3级各目标应一视同仁，加权系数相同，Wl3=W3。按给定的不等号方向，并为使计算机编程方便略去偏差变量中表示目标级的注脚符号不写而改为连续编号，得目标函数为

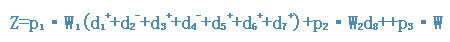（1）

规划的约束条件分4种。

1、配料质量指标约束第I产品配料结果必须合乎该产品各指标规定。指标是bki。

I=1,…,t,k=1，…，p                        (2)

有7 种化学成分含量，相应有p=7个质量指标，这种约束共有7个。Akj的值如下表所示。

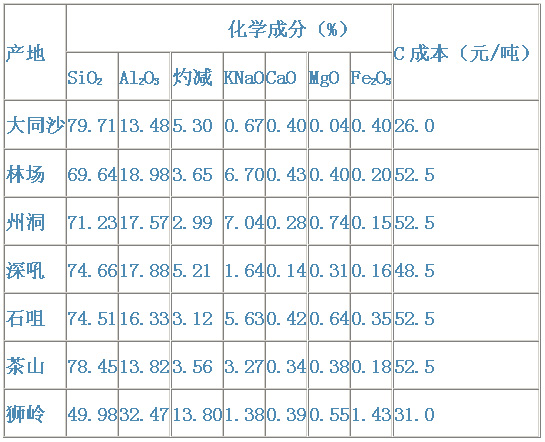
2、成本约束 第I产品配料不要超过计算时给出的期望成本值Ci

I=1,…，t        (3)

3、库存约束  某项原料用量不能超过该原料的库存量。

I=1,…，t,j=1…，n       (4)

4、均衡约束  所有原料配比之和为1。

如有人工加入的辅助配比，可从1减去此比值。其差作为均衡约束的右端值。

以上4个约束式中的变量均有Xij≥0，d+ji≥0，d-ji≥0,d+ji&S226;d-ji=0

对所有的j,I                      （6）

由上面的（1），（2），（3），（4），（5），（6）式构成了陶瓷坯料配料多目标模型。问题是，在（2）~（6）式的约束下求（1）式为极小。

由于目前还没有统一的国家产品质量的化学成分标准，故bki值只能按该产品的厂方历史数据来确定。值可在配料计算时给出。这对每种产品而言，该模型共有变量30个。其中决策变量n=7个，偏差变量共7+7+1+1+7=23个。约束式16个。其中等式约束1个，不等式约共7+1+7=15个。可见这只是个小规模问题，用一般微型计算机可以解决。